Combinations

Overview

A $k$ -combination of $n$ objects is an unordered “choice” of $k$ objects from the collection of $n$ objects. Alternatively viewed, it is a set of $k$ objects - ordering within a set does not matter. Combinations are derived by considering the number of $k$ -permutations of $n$ objects and discarding order, i.e. dividing by $k!$ . $(k n) = \frac{( n ) _{k}}{k !} = \frac{n !}{k ! ( n - k )!}$

void combinations_aux(
  const size_t n, int A[static n],
  const size_t k, int stack[static k],
  const size_t i
) {
  if (n < k) {
    return;
  }
  if (k == 0) {
    print_array(i, stack);
    return;
  }
  stack[i] = A[0];
  combinations_aux(n - 1, A + 1, k - 1, stack, i + 1);
  combinations_aux(n - 1, A + 1, k, stack, i);
}
 
void combinations(const size_t n, const size_t k, int A[static n]) {
  int *stack = calloc(k, sizeof(int));
  combinations_aux(n, A, k, stack, 0);
  free(stack);
}

The above approach prints out all $k$ -combinations of an array.

Pascal’s Triangle

A visual representation of the binomial coefficient’s is in the form of Pascal’s Triangle:

1
1   1
1   2   1
1   3   3   1
1   4   6   4   1
1   5  10  10   5   1
...

Terms are generated by adding the two terms above it, formalized via recurrence $(k n) = (k n - 1) + (k - 1 n - 1)$

Bit Strings

A bit string can be used to represent subsets of some finite set. A 1 value usually corresponds to inclusion in a subset, whereas a 0 value corresponds to exclusion. Thus, given set e.g. $A = {1, 2, 3, 4}$ , $011 0_{2}$ would correspond to subset ${2, 3}$ .

Bit strings also make it clear that the number of subsets with even cardinality must be equal to the number of subsets with odd cardinality. Hence, $(0 n) - (1 n) + \dots + (- 1)^{n} (n n) = 0$

Stars and Bars

The stars and bars chart refers to a graphical depiction of distributing $n$ objects (represented as $*$ ) into $m$ different buckets (delineated via $∣$ . An example chart looks like so: $* * ∣ * * * ∣ * ∣∣ *$

Notice there are $m - 1$ bars and interspersed amongst the $n$ stars. In the above example, there are $11$ total symbols, $4$ of which are bars, meaning there are $(4 11)$ ways to distribute the objects amongst the $5$ buckets. We can represent this using bit strings instead, with 0s as stars and 1s as bars. The above example is equivalently written as: $00100010110$

Lattice Paths

A lattice path is one of the shorted possible paths connecting two points on a lattice, moving only horizontally and vertically. By representing each horizontal move by 1 and each vertical move by 1, we see every lattice path has a corresponding bit string.

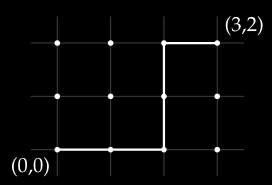
In this example, the total number of lattice paths from point $(0, 0)$ to $(3, 2)$ is therefore $(2 5) = (3 5)$ .

Binomial Coefficients

A binomial is a polynomial containing two terms. Consider $(x + y)^{n}$ . We see that term $x^{k} y^{n - k}$ maps to some bit string containing $k$ 1s and $n - k$ 0s. This might feel more obvious when expanding to $x \cdot x \dots x \cdot y \dots y$ . Since multiplication is commutative, the number of matching “bit strings” is the same as $(k n)$ .

Bibliography

Oscar Levin, Discrete Mathematics: An Open Introduction, 3rd ed., n.d., https://discrete.openmathbooks.org/pdfs/dmoi3-tablet.pdf.

My Notebook

Explorer